This page last modified 2004 March 10
The Three Functions of a Telescope
A telescope, when used for astronomy, serves three functions: it magnifies, it increases light grasp, and it increases resolution.
Magnification
Magnification is defined as (angle subtended by image)/(angle subtended by object). In an astronomical telescope this is almost exactly the same as (focal length of objective)/(focal length of eyepiece).
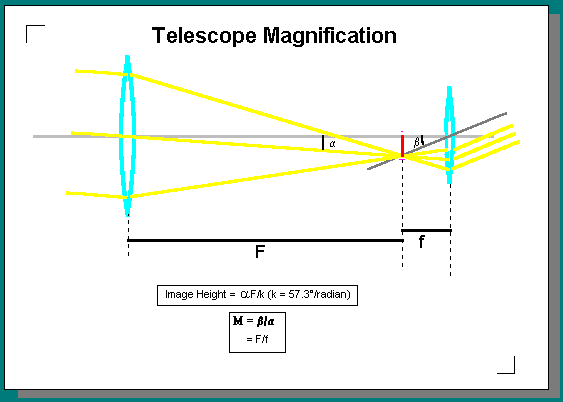
Limits to Magnification
The theoretical lower and upper useful limits to magnification are related to (amongst other things) the size of the exit pupil.
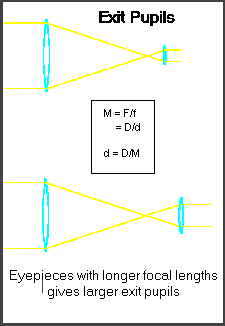
Lower Limit
One definition of the least useful magnification is when exit pupil diameter = eye pupil diameter. If exit pupil > δ, objective is being stopped down by pupil. It is, of course, perfectly possible to reduce the magnification even further, but extended objects will not get brighter. Also, if magnification is reduced too far in an obstructed telescope (e.g. Newtonian of Cassegrainian), the obstruction may become visible.
Hence lower useful limit of magnification, M', is given
by:
M' = D/δ
For middle-aged adult, δ~ 0.2";
M' = 5D, where D is in inches. [δ~5mm; M' = D/5, where
D is in mm]
Upper Limit
Increasing the magnification reduces the size of the exit pupil (and some of the aberrations of the eye's lens). Decreasing the exit pupil below about 0.03" (0.75mm) leads to a progressive impairment of vision.
The theoretical upper limit of magnification, M", is
therefore given by:
M" = D/0.03 or M" =
30D (D in inches)
It is also limited by the quality of the objective/primary and by the optical quality of short focal length eyepieces, which must have highly curved surfaces.
The impairment caused by small exit pupils may not affect vision so adversely as to preclude higher magnifications — indeed, the eye's aberrations may be attenuated by very small exit pupils. The "rule of thumb" is 50D (which is often the most, or more than, the atmosphere will permit), although over 70D may be possible sometimes for close double-stars. Some observers use up to about 140D, but these high magnifications probably compensate for a lack of visual acuity. Very high magnifications may be useful when averted vision is used for the same reason (reduced acuity).
Resolution
The minimum magnification, Mr, for at which the image at the focal plane is fully resolved by the eye is 13D inches (or half the diameter of objective in mm). The comments above on increasing magnification to compensate for less-than-perfect visual acuity apply here as well.
Light Grasp and Limiting Magnitude
Quantity of light concentrated by objective at primary focus — function of D, not of focal length or magnification. It is more meaningfully defined as relative intensity of light from point source passed to retina by optical train, and by naked eye.
If eye's pupil, δ, is not
smaller than exit pupil, then light grasp is:
(D2/ δ2) × τ
where τ is the transmission factor
of instrument.
Tables of light grasp are misleading because:
- Observations and assumptions from which the table was constructed may be inapplicable to other conditions
- Atmospheric seeing can render small instruments able to see fainter objects than larger ones
- Most telescopes and all observers are not "normal"
- Magnification will affect the outcome
- Direct or averted vision
- Type of telescope (loss of light in 2° spectrum)
- Bright field objects affect dark adaptation
Theoretical limiting magnitude can be calculated:
Under mag 6.5 skies:
theoretical limiting mag = 6.5 - 5 logδ + 5 log D
(This is low by about 1.5 mag for apertures <20")
Extended Objects
No passive optical instrument can increase the brightness per unit area of an extended object.
Light passed to image at prime focus will be
D2 × t / δ2
times as great as that received by
the retina of the naked eye.
When the telescope is used with magnification, M, the
illuminated area of the retina is increased by M2. Hence
the apparent brightness of the image is increased by
(D2 × t) / (M2 × δ2)
......... (1)
But the minimum magnification, M', to utilise the light grasp of the objective is D/δ. Substituting for M in equation (1), we find that the telescopic image is τ times the naked eye image. Since τ < 1, the brightness of an extended object cannot be increased by a telescope.
Resolution
Diffraction affects the edge of a pencil of light. As a consequence, some light from a point source is spread away from the image. Destructive and constructive interference results in a disc of light (the Airy disc), surrounded by diffraction rings of decreasing brightness.

Assuming the optics are diffraction-limited, the radius of the Airy
disk, A, is given by:
A = 1.22λ/D radians
where λ is the
wavelength of light.
For λ = 555 nm (yellow light), this reduces to:
A = 140/D arcsec
where D is in mm.
The Dawes Criterion (Dawes Limit) is an empirically derived
value for the separation at which a pair of stars is just resolvable as a pair.
This is 115.82 / D arcsec, when D is in mm.
In practice, the
atmosphere usually limits the resolution to anything from 2 to 10 arcsec (or
worse). A typical good site may attain seeing of 1 arcsec.
Telescopes on Mauna Kea sometimes attain 0.25 arcsec.
Hubble Space Telescope attains 0.05 arcsec.
You may use this form to calculate the resolution of a telescope (λ = 555 nm)
Type the aperture into the box, then click in one of the boxes below.
Acknowledgements and Apology: My grateful thanks go to Ed Zarenski, who noticed an error in an equation in the section on Resolution. My apologies go to all those who were misled by the error during the 5 years before Ed noticed it!


